KMP算法主要解决什么样的问题?
KMP算法主要解决关键字搜索,也就是字符串匹配的这类问题。
给你两个字符串A和B,其中A字符串包含着B字符串,找到B字符串在A中的位置
如下面的两个字符串:
char *str = "bacbababadababacambabacaddababacasdsd";char *ptr = "ababaca";
str有两处包含ptr
分别在str的下标10,26处包含ptr。“bacbababadababacambabacaddababacasdsd”;\

算法说明:
一般匹配字符串时,我们从目标字符串str(假设长度为n)的第一个下标选取和ptr长度(长度为m)一样的子字符串进行比较,如果一样,就返回开始处的下标值,不一样,选取str下一个下标,同样选取长度为n的字符串进行比较,直到str的末尾(实际比较时,下标移动到n-m)。这样的时间复杂度是O(n*m)。
KMP算法怎么简化时间复杂度?
充分利用了目标字符串ptr的性质(比如里面部分字符串的重复性,即使不存在重复字段,在比较时,实现最大的移动量)。
考察目标字符串ptr:
ababaca 这里我们要计算一个长度为m的转移函数next。next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。
比如:abcjkdabc,那么这个数组的最长前缀和最长后缀相同必然是abc。
cbcbc,最长前缀和最长后缀相同是cbc。 abcbc,最长前缀和最长后缀相同是不存在的。**注意最长前缀:是说以第一个字符开始,但是不包含最后一个字符。
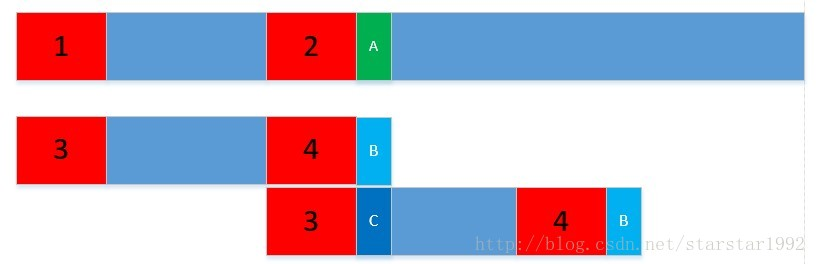
比如aaaa相同的最长前缀和最长后缀是aaa。** 对于目标字符串ptr,ababaca,长度是7,所以next[0],next[1],next[2],next[3],next[4],next[5],next[6]分别计算的是 a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀的长度。由于a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀是“”,“”,“a”,“ab”,“aba”,“”,“a”,所以next数组的值是[-1,-1,0,1,2,-1,0],这里-1表示不存在,0表示存在长度为1,2表示存在长度为3。这是为了和代码相对应。下图中的1,2,3,4是一样的。1-2之间的和3-4之间的也是一样的,我们发现A和B不一样;之前的算法是我把下面的字符串往前移动一个距离,重新从头开始比较,那必然存在很多重复的比较。现在的做法是,我把下面的字符串往前移动,使3和2对其,直接比较C和A是否一样。

#includeusing namespace std;void cal_next(char *ptr, int *next, int plen){ next[0] = -1; //next[0]默认置为-1 int k = -1; // 设置匹配开始位 for (int q = 1; q <= plen - 1; q++) //在字符串里循环比较 { while (k > -1 && ptr[k + 1] != ptr[q]){ //两个字符之间不同 k = next[k]; //k值回溯 } if (ptr[k + 1] == ptr[q]){ //两个字符相同 k = k + 1; // 比较下一个字符 } next[q] = k; // 将k值放置在数组里 }}int KMP(char *str, int slen, char *ptr, int plen){ int *next = new int[plen]; //新建数组 cal_next(ptr, next, plen); //计算ptr的数组 int k = -1; //设置ptr匹配开始位 for (int i = 0; i < slen; i++) //str和pt开始匹配 { while (k>-1 && ptr[k + 1] != str[i]) //str和ptr对应的字符不匹配 k = next[k]; //K值回溯 if (ptr[k + 1] == str[i]) // str和ptr的字符相匹配 { k = k + 1; //K值加1,匹配第二个字符 } if (k == plen - 1) { return i - plen + 1; // 返回匹配成功后的ptr字符串的位置 } }}int main(){ char *str = "sutaoyu01"; char *ptr = "oyu"; int slen = 9; int plen = 3; int len = KMP(str, 9, ptr, 3); cout << len<<","<